Appendix D
JAPE: Implementation [#]
The annual Diagram prize for the oddest book title of the year has been awarded to Gerard Forlin’s Butterworths Corporate Manslaughter Service, a hefty law tome providing guidance and analysis on corporate liability for deaths in the workplace.
The book, not published until January, was up against five other shortlisted titles: Fancy Coffins to Make Yourself; The Flat-Footed Flies of Europe; Lightweight Sandwich Construction; Tea Bag Folding; and The Art and Craft of Pounding Flowers: No Paint, No Ink, Just a Hammer! The shortlist was thrown open to readers of the literary trade magazine The Bookseller, who chose the winner by voting on the magazine’s website. Butterworths Corporate Manslaughter Service, a snip at 375, emerged as the overall victor with 35% of the vote.
The Diagram prize has been a regular on the award circuit since 1978, when Proceedings of the Second International Workshop on Nude Mice carried off the inaugural award. Since then, titles such as American Bottom Archaeology and last year’s winner, High-Performance Stiffened Structures (an engineering publication), have received unwonted publicity through the prize. This year’s winner is perhaps most notable for its lack of entendre.
Manslaughter Service kills off competition in battle of strange titles, Emma Yates, The Guardian, November 30, 2001.
This appendix gives implementation details and formal definitions of the JAPE annotation patterns language. Section D.1 gives a more formal definition of the JAPE grammar, and some examples of its use. Section D.2 describes JAPE’s relation to CPSL. Section D.3 describes the initialisation of a JAPE grammar, Section D.4 talks about the execution of JAPE grammars, and the final section explains how to switch the Java compiler used for JAPE.
D.1 Formal Description of the JAPE Grammar [#]
JAPE is similar to CPSL (a Common Pattern Specification Language, developed in the TIPSTER programme by Doug Appelt and others), with a few exceptions. Figure D.1 gives a BNF (Backus-Naur Format) description of the grammar.
An example rule LHS:
( ({Token.kind == "containsDigitAndComma"}):number
{Token.string == "kilograms"} ):whole
A basic constraint specification appears between curly braces, and gives a conjunction of annotation/attribute/value specifiers which have to match at a particular point in the annotation graph. A complex constraint specification appears within round brackets, and may be bound to a label with the ‘:’ operator; the label then becomes available in the RHS for access to the annotations matched by the complex constraint. Complex constraints can also have Kleene operators (*, +, ?) applied to them. A sequence of constraints represents a sequential conjunction; disjunction is represented by separating constraints with ‘|’.
Converted to the format accepted by the JavaCC LL parser generator, the most significant fragment of the CPSL grammar (as described by Appelt, based on an original specification from a TIPSTER working group chaired by Boyan Onyshkevych) goes like this:
(patternElement)+ ("|" (patternElement)+ )*
patternElement -->
"{" constraint ("," constraint)* "}"
| "(" constraintGroup ")" (kleeneOp)? (binding)?
Here the first line of patternElement is a basic constraint, the second a complex one.
( <multiphase> <ident> )?
( ( ( JavaImportBlock )
( ( ControllerStartedBlock )
| ( ControllerFinishedBlock )
| ( ControllerAbortedBlock )
)*
( SinglePhaseTransducer )+ ) |
( <phases> ( <path> )+ ) )
<EOF>
SinglePhaseTransducer ::=
<phase> <ident>
( ( <input> ( <ident> )* ) |
( <option> ( <ident> <assign> ( <ident> | <bool> ) )* ) )*
( ( Rule ) | MacroDef | TemplateDef )*
JavaImportBlock ::= ( <javaimport> <leftBrace> ConsumeBlock )?
ControllerStartedBlock ::= ( <controllerstarted> <leftBrace> ConsumeBlock )
ControllerFinishedBlock ::= ( <controllerfinished> <leftBrace> ConsumeBlock )
ControllerAbortedBlock ::= ( <controlleraborted> <leftBrace> ConsumeBlock )
Rule ::=
<rule> <ident>
( <priority> <integer> )?
LeftHandSide "-->" RightHandSide
MacroDef ::= <macro> <ident> ( PatternElement | Action )
TemplateDef ::= <template> <ident> <assign> AttrVal
LeftHandSide ::= ConstraintGroup
ConstraintGroup ::= ( PatternElement )+ ( <bar> ( PatternElement )+ )*
PatternElement ::= ( <ident> | BasicPatternElement | ComplexPatternElement )
BasicPatternElement ::=
( ( <leftBrace> Constraint ( <comma> Constraint )* <rightBrace> ) |
( <string> ) )
ComplexPatternElement ::=
<leftBracket> ConstraintGroup <rightBracket>
( KleeneOperator )?
( <colon> ( <ident> | <integer> ) )?
KleeneOperator ::=
( <kleeneOp> ) |
( <leftSquare> ( <integer> ( <comma> <integer> )? ) <rightSquare> )
Constraint ::=
( <pling> )? <ident>
( ( FeatureAccessor <attrOp> AttrVal )
| ( <metaPropOp> <ident> <attrOp> AttrVal )
| ( <ident> ( ( <leftBrace> Constraint <rightBrace> ) | ( Constraint ) ) )
)?
FeatureAccessor ::= ( <period> <ident> )
AttrVal ::= ( ( <string> | <ident> | <integer> | <floatingPoint> | <bool> ) )
| ( TemplateCall )
TemplateCall ::= <leftSquare> <ident>
( <ident> <assign> AttrVal ( <comma> )? )*
<rightSquare>
RightHandSide ::= Action ( <comma> Action )*
Action ::= ( NamedJavaBlock | AnonymousJavaBlock | AssignmentExpression | <ident> )
NamedJavaBlock ::= <colon> <ident> <leftBrace> ConsumeBlock
AnonymousJavaBlock ::= <leftBrace> ConsumeBlock
AssignmentExpression ::=
( <colon> | <colonplus> ) <ident> <period> <ident> <assign>
<leftBrace>
( <ident> <assign>
( AttrVal |
( <colon>
<ident>
( ( <period> <ident> ( <period> | <metaPropOp> ) <ident> ) |
( <metaPropOp> <ident> )
)
)
)
( <comma> )?
)*
<rightBrace>
appendSpecials ::= java code
ConsumeBlock ::= java code
An example of a complete rule:
( ( {Token.kind == "number"} )+:numbers {Token.kind == "unit"} )
-->
:numbers.Name = { rule = "NumbersAndUnit" }
This says ‘match sequences of numbers followed by a unit; create a Name annotation across the span of the numbers, and attribute rule with value NumbersAndUnit’.
D.2 Relation to CPSL [#]
We differ from the CPSL spec in various ways:
- No pre- or post-fix context is allowed on the LHS.
- No function calls on the LHS.
- No string shorthand on the LHS.
- We have multiple rule application algorithms (see Section 8.4).
- Expressions relating to labels unbound on the LHS are not evaluated on the RHS. (In TextPro they evaluate to ‘false’.)
- JAPE allows arbitrary Java code on the RHS.
- JAPE has a different macro syntax, and allows macros for both the RHS and LHS.
- JAPE grammars are compiled and can be stored as serialised Java objects.
Apart from this, it is a full implementation of CPSL, and the formal power of the languages is the same (except that a JAPE RHS can delete annotations, which straight CPSL cannot). The rule LHS is a regular language over annotations; the rule RHS can perform arbitrary transformations on annotations, but the RHS is only fired after the LHS been evaluated, and the effects of a rule application can only be referenced after the phase in which it occurs, so the recognition power is no more than regular.
D.3 Initialisation of a JAPE Grammar [#]
When a JAPE grammar is loaded in GATE, each phase is converted into a finite state machine, a process that has several stages. Each rule is treated as a regular expression using annotation-based patterns as input symbols. A JAPE phase is a disjunction of rules, so it is also a regular expression. The first stage of building the associated FSM for a JAPE phase is the construction of a non-deterministic finite-state automaton, following the algorithm described in [Aho et al. 86].
Additional to standard regular expressions, JAPE rules also contain bindings (labels associated to pattern segments). These are intended to be associated to the matched input symbols (i.e. annotations) during the matching process, and are used while executing the actions caused by the rule firing. Upon creating the equivalent FSM for a given JAPE rule, bindings are associated with the FSM transitions. This changes the semantics of a transition – besides moving the state machine into a new current state, a transition may also bind the consumed annotation(s) with one or more labels.
In order to optimise the execution time during matching (at the expense of storage space), NFAs are usually converted to Deterministic Finite State Automata (DFAs) using e.g. the subset algorithm [Aho et al. 86]. In the case of JAPE this transformation is not possible due to the binding labels: two or more transitions from the NFA that match the same annotation pattern cannot be compacted into a single transition in the DFA if they have different bindings. Because of this, JAPE grammars are represented as non-deterministic finite state machines. A partial optimisation that eliminates the ϵ-transitions from the NFA is however performed.
The actions represented on the right hand side of JAPE rules are converted to compiled Java classes and are associated with final states in the FSM. The final in-memory representation of a JAPE grammar thus consists of a non-deterministic finite state machine, with transitions that use annotation-based patterns as input symbols, additionally marked with bindings information and for which the final states are associated with actions.
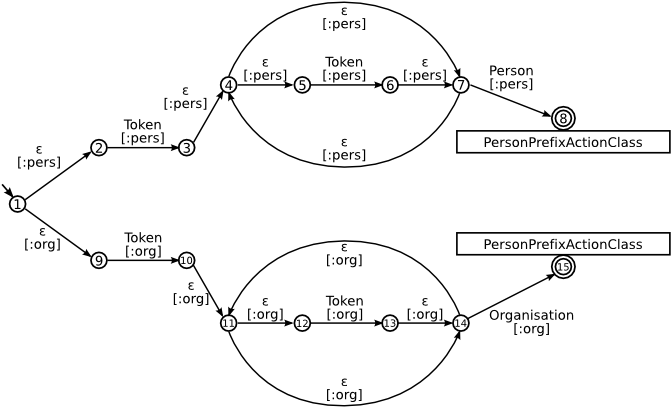
Starting from the following two JAPE rules:
(
({Token})+ {Person}
):pers
--> {...}
Rule: OrganisationPrefix (
({Token})+ {Organisation}
):org --> {...}
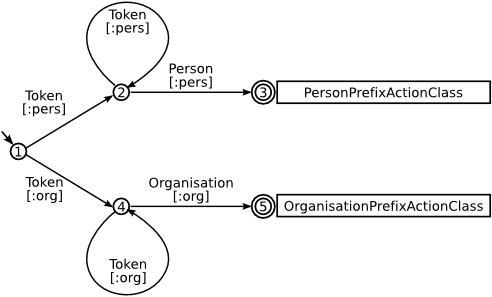
the associated NFA is constructed, as illustrated in Figure D.2. Note that due to the fact that the final states are associated with different actions, they cannot be joined into a single one and are kept separate. This automaton is then optimised by eliminating the ϵ-transitions, resulting in the NFA presented in Figure D.3. For the sake of simplicity, the annotation patterns used are the most basic ones, depending solely on annotation type. In the graphical representation, the transitions are marked with the type of annotation that they match and the associated binding in square brackets.
It can be observed in Figure D.3 that there are two transitions starting from state 1 (leading to states 2, respectively 4) that both consume annotations of type Token, thus even the optimised finite state machine is still non-deterministic.
Once a JAPE grammar is converted to the equivalent finite state automaton, the initialisation phase is complete.
D.4 Execution of JAPE Grammars [#]
The execution of a JAPE grammar can be described in simple terms as finding a path through an annotation graph where all the annotations traversed form a sequence that is accepted by the finite state machine built during the initialisation phase. The actual process is somewhat more complex than that, as it also needs to take into account the various matching modes, the filtering of input annotation types, to deal with the assignment of matched annotation to bindings, and to manage the execution of actions whenever successful matches occur.
Executing a JAPE grammar involves simulating the execution of a non-deterministic finite state automaton (NFA) while using an annotation graph as input. At each step we start from a document position (initially zero) and a finite state machine in a given state (initially the start state). Annotations found at the given document position are compared with the restrictions encoded in the NFA transitions; if they match, the annotations are consumed and the state machine moves to a new state. Ambiguities are possible at each step both in terms of input (several matching annotations can start at the same offset) and in terms of available NFA transitions (the state machine is non-deterministic, so multiple transitions with the same restrictions can be present). When such ambiguities are encountered, the current state machine is cloned to create as many copies as necessary, and each such copy continues the matching process independently. The JAPE executor thus needs to keep track of a family of state machines that are running in parallel – henceforth we shall call these FSM instances.
Whenever one of the active FSM instances is moved to a new state, a test is performed to check if the new state is a final one. If that is the case, the FSM instance is said to be in an accepting state, and a copy of its state is saved for later usage.
When none of the active FSM instances can advance any further, the stored accepting FSM instances are used to execute JAPE actions, according to the declared matching style of the current grammar.
A high-level view1 of the algorithm used during the execution of a JAPE grammar is presented in Listing D.1, in a Java-inspired pseudo-code.
2currentDocPosition = 0;
3activeFSMInstances = new List<FSMInstance>();
4acceptingFSMInstances = new List<FSMInstance>();
5while(currentDocPosition < document.length()){
6 //create an initial FSM instance, starting from
7 //the current document position
8 activeFSMInstances.add(
9 new FSMInstance(currentDocPosition));
10 //advance all FSM instances,
11 //until no further advance is possible
12 while(!activeFSMInstances.isEmpty()){
13 FSMInstance aFSM = activeFSMInstances.remove(0);
14 //advance aFSM, consuming annotations, linking used
15 //annotations to binding labels, as required;
16
17 //create cloned copies as necessary and add them to
18 //activeFSMInstances;
19
20 //save any accepting state of aFSM
21 //into acceptingFSMInstances;
22 }
23 if(!acceptingFSMInstances.isEmpty()){
24 //execute the action(s)
25 }
26
27 //move to the new document position, in accordance
28 //with the matching style.
29}
The next paragraphs contain some more detailed comments, indexed using the line numbers in the listing:
- line 1
- The annotations present in the document are filtered according to the Input declaration in the JAPE code, if one was present. This causes the JAPE executor to completely ignore annotations that are not listed as valid input.
- lines 2–4
- The matching process is initialised by setting the document position to 0, and creating empty lists of active and accepting FSM instances.
- lines 5–29
- The matching continues until all the document text is exhausted.
- line 8
- Each step starts from the current document position with a single FSM instance.
- lines 12–22
- While there are still active FSM instances, they are advanced as far as possible. Whenever ambiguities are encountered, cloned copies are created and added to the list of active FSM instances. Whenever an FSM instance reaches a final state during its advancing, a copy of its state is saved to the list of accepting FSM instances.
- lines 23–25
- This segment of code is reached when there are no more active FSM instances
– all active instances were advanced as far as possible and either saved to the accepting
list (if they reached a final state during that process) or simply discarded (if they could
advance no further but they still have not reached a final state).
At this point, any successful matches that occurred need to be acted upon, so the list of accepting FSM instances is inspected. If there are any, their associated actions are now executed, according to the desired matching style. For instance if the matching style used is Appelt, then only the accepting FSM instance that has covered the most input will be executed; conversely, if the matching style is Brill, then all accepting FSM instances will have their actions executed, etc. - line 27
- When this point is reached, all possible matches from the current document position were found and the required action executed. The next step is to move to the next starting position in the document, and re-start the matching process from there. Depending on the matching style selected, the new document position is either the oldPosition + 1, in the case of All, or matchingEndPosition + 1 in all other cases.
D.5 Using a Different Java Compiler [#]
GATE allows you to choose which Java compiler is used to compile the action classes generated from JAPE rules. The preferred compiler is specified by the Compiler_type option in gate.xml. At present the supported values are:
- Sun
- The Java compiler supplied with the JDK. Although the option is called Sun, it supports any JDK that supplies com.sun.tools.javac.Main in a standard location, including the IBM JDK (all platforms) and the Apple JDK for Mac OS X.
- Eclipse
- The Eclipse compiler, from the Java Development Tools of the Eclipse project2. Currently we use the compiler from Eclipse 3.2, which supports Java 5.0.
By default, the Eclipse compiler is used. It compiles faster than the Sun compiler, and loads dependencies via the GATE ClassLoader, which means that Java code on the right hand side of JAPE rules can refer to classes that were loaded from a plugin JAR file. The Sun compiler can only load classes from the system classpath, so it will not work if GATE is loaded from a subsidiary classloader, e.g. a Tomcat web application. You should generally use the Eclipse compiler unless you have a compelling reason not to.
Support for other compilers can be added, but this is not documented here - if you’re in a position to do this, you won’t mind reading the source code...
1The view of the algorithm presented here is greatly simplified, for the sake of clarity. The actual implementation consists of a few thousand lines of Java code.