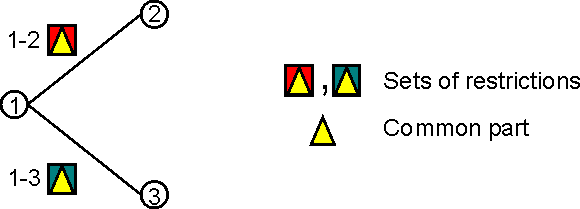Appendix B
JAPE: Implementation [#]
The annual Diagram prize for the oddest book title of the year has been awarded to Gerard Forlin’s Butterworths Corporate Manslaughter Service, a hefty law tome providing guidance and analysis on corporate liability for deaths in the workplace.
The book, not published until January, was up against five other shortlisted titles: Fancy Coffins to Make Yourself; The Flat-Footed Flies of Europe; Lightweight Sandwich Construction; Tea Bag Folding; and The Art and Craft of Pounding Flowers: No Paint, No Ink, Just a Hammer! The shortlist was thrown open to readers of the literary trade magazine The Bookseller, who chose the winner by voting on the magazine’s website. Butterworths Corporate Manslaughter Service, a snip at 375, emerged as the overall victor with 35
The Diagram prize has been a regular on the award circuit since 1978, when Proceedings of the Second International Workshop on Nude Mice carried off the inaugural award. Since then, titles such as American Bottom Archaeology and last year’s winner, High-Performance Stiffened Structures (an engineering publication), have received unwonted publicity through the prize. This year’s winner is perhaps most notable for its lack of entendre.
Manslaughter Service kills off competition in battle of strange titles, Emma Yates, The Guardian, November 30, 2001.
This chapter gives implementation details and formal definitions of the JAPE annotation patterns language. Section B.1 gives a more formal definition of the JAPE grammar, and some examples of its use. Section B.2 describes JAPE’s relation to CPSL. The next 3 sections describe the algorithms used, label binding, and the classes used. Section B.6 gives an example of the implementation; and finally, section B.7 explains the compilation process.
B.1 Formal Description of the JAPE Grammar [#]
JAPE is similar to CPSL (a Common Pattern Specification Language, developed in the TIPSTER programme by Doug Appelt and others), with a few exceptions. Figure B.1 gives a BNF (Backus-Naur Format) description of the grammar.
An example rule LHS:
Rule: KiloAmount
( ({Token.kind == "containsDigitAndComma"}):number {Token.string == "kilograms"} ):whole |
A basic constraint specification appears between curly braces, and gives a conjunction of annotation/attribute/value specifiers which have to match at a particular point in the annotation graph. A complex constraint specification appears within round brackets, and may be bound to a label with the “:” operator; the label then becomes available in the RHS for access to the annotations matched by the complex constraint. Complex constraints can also have Kleene operators (*, +, ?) applied to them. A sequence of constraints represents a sequential conjunction; disjunction is represented by separating constraints with “|”.
Converted to the format accepted by the JavaCC LL parser generator, the most significant fragment of the CPSL grammar (as described by Appelt, based on an original specification from a TIPSTER working group chaired by Boyan Onyshkevych) goes like this:
constraintGroup -->
(patternElement)+ ("|" (patternElement)+ )* patternElement --> "{" constraint ("," constraint)* "}" | "(" constraintGroup ")" (kleeneOp)? (binding)? |
Here the first line of patternElement is a basic constraint, the second a complex one.
An example of a complete rule:
Rule: NumbersAndUnit
( ( {Token.kind == "number"} )+:numbers {Token.kind == "unit"} ) --> :numbers.Name = { rule = "NumbersAndUnit" } |
This says ‘match sequences of numbers followed by a unit; create a Name annotation across the span of the numbers, and attribute rule with value NumbersAndUnit’.
B.2 Relation to CPSL [#]
We differ from the CPSL spec in various ways:
- No pre- or post-fix context is allowed on the LHS.
- No function calls on the LHS.
- No string shorthand on the LHS.
- We have two rule application algorithms (one like TextPro, one like Brill/Mitre). See section B.3.
- Expressions relating to labels unbound on the LHS are not evaluated on the RHS. (In TextPro they evaluate to “false”.) See the binding scheme description in section B.4.
- JAPE allows arbitrary Java code on the RHS.
- JAPE has a different macro syntax, and allows macros for both the RHS and LHS.
- JAPE grammars are compiled and stored as serialised Java objects.
Apart from this, it is a full implementation of CPSL, and the formal power of the languages is the same (except that a JAPE RHS can delete annotations, which straight CPSL cannot). The rule LHS is a regular language over annotations; the rule RHS can perform arbitrary transformations on annotations, but the RHS is only fired after the LHS been evaluated, and the effects of a rule application can only be referenced after the phase in which it occurs, so the recognition power is no more than regular.
B.3 Algorithms for JAPE Rule Application [#]
JAPE rules are applied in one of two ways: Brill-style, where each rule is applied at every point in the document at which it matches; Appelt-style, where only the longest matching rule is applied at any point where more than one might apply.
In the Appelt case, the rule set for a phase may be considered as a single disjunctive expression (and an efficient implementation would construct a single automaton to recognise the whole rule set). To solve this problem, we need to employ two algorithms:
- one that takes as input a CPSL representation and builds a machine capable of recognizing the situations that match the rules and makes the bindings that occur each time a rule is applied. This machine is a Finite State Machine (FSM), somewhat similar to a lexical analyser (a deterministic finite state automaton).
- another one that uses the FSM built by the above algorithm and traverses the annotation graph in order to find the situations that the FSM can recognise.
B.3.1 The first algorithm
The first step that needs to be taken in order to create the FSM is to read the CPSL description from the external file(s). This is already done in the old version of Jape.
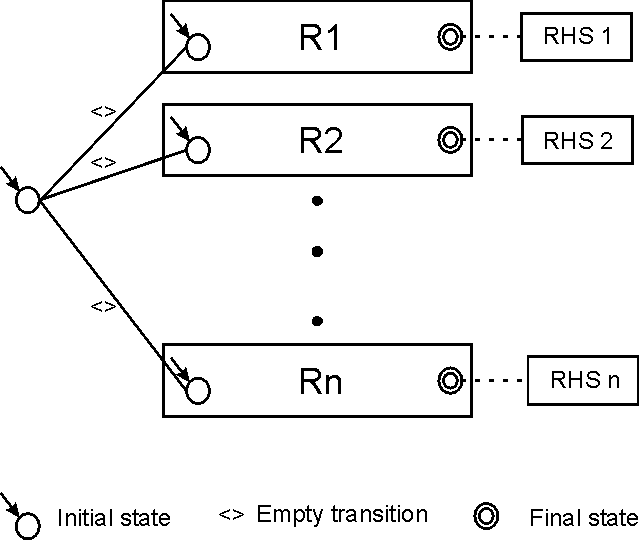
The second step is to build a nondeterministic FSM from the java objects resulted from the parsing process. This FSM will have one initial state and a set of final states, each of them being associated to one rule (this way we know what RHS we have to execute in case of a match). The nondeterministic FSM will also have empty transitions (arcs labeled with nil). In order to build this FSM we will need to implement a version of the algorithm used to convert regular expressions in NFAs.
Finally, this nondeterministic FSM will have to be converted to a deterministic one. The deterministic FSM will have more states (in the worst case s! (where s is the number of states in the nondeterministic one); this case is very improbable) but will be more efficient because it will not have to backtrack.
Let NFSM be the nondeterministic FSM and DFSM the deterministic one.
|
|
The issues that have to be addressed are:
The NFSM will basically be a big OR. This means that it will have an initial state from which empty transitions will lead to the sub-FSMs associated to each rule (see Fig. B.2). When the NFSM is converted to a DFSM the initial state will be the set containing all the initial states of the FSMs associated to each rule. From that state we will have to compute the possible transitions. For this, the classical algorithm requires us to check for each possible input symbol what is the set of reachable states. The problem is that our input symbols are actually sets of restrictions. This is similar to an automaton that has an infinite set of input symbols (although any given set of rules describes a finite set of constraints). This is not so bad, the real problem is that we have to check if there are transitions that have the same restrictions. We can safely consider that there are no two transitions with the same set of restrictions. This is safe because if this assumption is wrong, the result will be a state that has two transitions starting from it, transitions that consume the same symbol. This is not a problem because we have to check all outgoing transitions anyway; we will only check the same transition twice.
This leads to the next issue. Imagine the next part of the transition graph of a FSM (Fig. B.3):
|
|
The restrictions associated to a transition are depicted as graphical figures (the two coloured squares). Now imagine that the two sets of restrictions have a common part (the yellow triangle).
Let us assume that at one moment the current node in the FSM graph (for one of the active FSM instances) is state 1. We get from the annotation graph the set of annotations starting from the associated current node in the annotation graph and try to advance in the FSM transition graph. In order to do this we will have to find a subset of annotations that match the restrictions for moving to state 2 or state 3. In a classical algorithm what we would do is to try to match the annotations against the restrictions “1-2” (this will return a boolean value and a set of bindings) and then we will try the matching against the restrictions “1-3” this means that we will try to match the restrictions in the common part twice. Because of the probable structure of the FSM transition graph there will be a lot of transitions starting from the same node which means that may be a lot of conditions checked more than one times.
What can we do to improve this?
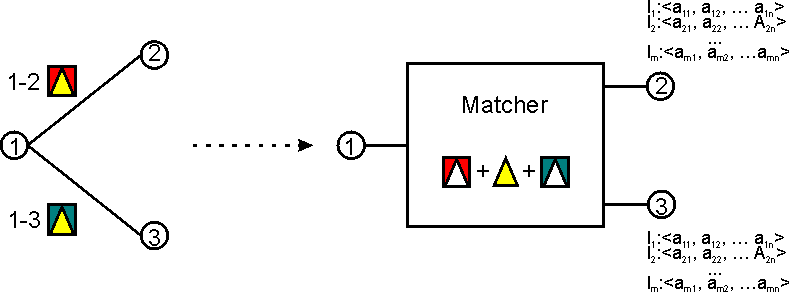
We need a way to combine all the restrictions associated to all outgoing arcs of a state (see Fig. B.4).
|
|
One way to do the (combined) matching is to pre-process the DFSM and to convert all transitions to matchers (as in Fig. B.4). This could be done using the following algorithm:
- Input: A DFSM;
- Output: A DFSM with compound restrictions checks.
- for each state s of the DFSM
- collect all the restrictions in the labels of the outgoings arcs from s (in the DFSM
transition graph)
Note: these restrictions are either of form “Type == t1” or of form “Type == t1 && Attri == V aluei - Group all these restrictions by type and branch and create compound restrictions
of form “[Type == t1 && Attr1 == V alue1 && Attr2 == V alue2 && ... &&
Attrn == V aluen]”
The grouping has to be done with care so it doesn’t mix restrictions from different branches, creating unnecessary restrictive queries. These restrictions will be sent to the annotation graph which will do the matching for us. Note that we can only reuse previous queries if the restrictions are identical on two branches.1
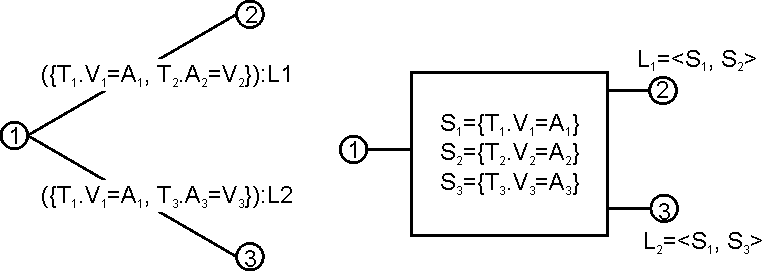
- Create the data structures necessary for linking the bindings to the results of the queries (see Fig B.5)
- collect all the restrictions in the labels of the outgoings arcs from s (in the DFSM
transition graph)
|
|
When this machine will be used for the actual matching the three queries will be run and the results will be stored in sets of annotations (S1..S3 in the picture) and...
- For each pair of annotations from (A1, A2) s.t. A1 in S1 & A2 in S2
- a new DFSM instance will be created;
- this instance will move to state 2;
- ¡A1, A2¿ will be bound to L1
- the corresponding node in the annotation graph will become max(A1 endNode(), A2.endNode()).
- Similarly, for each pair of annotations from (A1, A3) s.t. A1 in S1 & A3 in S3
- a new DFSM instance will be created;
- this instance will move to state 3;
- ¡A1, A3¿ will be bound to L2
- the corresponding node in the annotation graph will become max(A1.endNode(), A3.endNode()).
While building the compound matcher it is possible to detect queries that depend one from another (e.g. if the expected results of a query are a subset of the results from another query). This kind of situations can be marked so when the queries are actually run some operations can be avoided (e.g. if the less restrictive search returned no results than the more restrictive one can be skipped, or if a search returns an AnnotationSet (an object that can be queried) than the more restrictive query can be.
B.3.2 Algorithm 2
Consider the following figure:
|
|
Basically, the algorithm has to traverse this graph starting from the leftmost node to the rightmost one. Each path found is a sequence of possible matches.
Because more than one annotation (all starting at the same point) can be matched at one step, a
path is not viewed as a classical path in a graph, but a sequence of steps, each step being a set of
annotations that start in the same node.
e.g. a path in the graph above can be: [1].[2,4].[7,8].[10];
Note that the next step continues from the rightmost node reached by the annotations in the current
step.
The matchings are made by a Finite State Machine that resembles an clasical lexical analyser (aka. scanner). The main difference from a scanner is that there are no input symbols; the transition from one state to another is based on matching a set of objects (annotations) against a set of restrictions (the constraint group in the LHS of a CPSL rule).
The algorithm can be the following:
- startNode = the leftmost node
- create a first instance of the FSM and add it to the list of active instances;
- for this FSM instance set current node as the leftmost node;
- while(startNode != last node) do
- while (not over) do
- for each Fi active instance of the FSM do
- if this instance is in a final state then save a clone of it in the set of accepting FSMs (instances of the FSM that have reached a final state);
- read all the annotations starting from the current node;
- select all sets of annotation that can be used to advance one step in the transition graph of the FSM;
- for each such set create a new instance of the FSM, put it in the active list and make it consume the corresponding set of annotations, making any necessary bindings in the process (this new instance will advance in the annotation graph to the rightmost node that is an end of a matched annotation);
- discard Fi;
- end for;
- if the set of active instances of FSM is empty * then over = true;
end while;
- for each Fi active instance of the FSM do
- if the set of accepting FSMs is not empty
- from all accepting FSMs select ** the one that matched the longest path;if there are more than one for the same path length select the one with highest priority;
- execute the action associated to the final state of the selected FSM instance;
- startNode = selectedFSMInstance.getLastNode.getNextNode();
- else //the matching failed → start over from the next node // startNode = startNode.getNextNode();
- while (not over) do
- end while;
*: the set of active FSM instances can decrease when an active instance cannot continue (there is no set of annotations starting from its current node that can be matched). In this case it will be removed from the set.
**: if we do Brill style matching, we have to process each of the accepting instances.
B.4 Label Binding Scheme [#]
In TextPro, a “:” label binds to the last matched annotation in its scope. A “+:” label binds to all the annotations matched in the scope. In JAPE there is no “+:” label (though there is a “:+” – see below), due to the ambiguity with Kleene +. In CPSL a constraint group can be both labelled and have a Kleene operator. How can Kleene + followed by label : be distinguished from label +: ? E.g. given (....)+:label are the constraints within the brackets having Kleene + applied to them and being labelled, or is it a +: label?
Appelt’s answer is that +: is always a label; to get the other interpretation use ((...)+):. This may be difficult for rule developers to remember; JAPE disallows the “+:” label, and makes all matched annotations available from every label.
JAPE adds a “:+” label operator, which means that all the spans of any annotations matched are assigned to new annotations created on the RHS relative to that label. (With ordinary “:” labels, only the span of the outermost corners of the annotations matched is used.) (This operator disappears in GATE version 2, with the elimination of multi-span annotations.)
Another problem regards RHS interpretation of unbound labels. If we have something like
(
( {Word.string == "thing"} ):1 | ( {Word.string == "otherthing"} ):2 ) |
on the LHS, and references to :1 and :2 on the RHS, only one of these will actually be bound to anything when the rule is fired. The expression containing the other should be ignored. In TextPro, an assignment on the RHS that references an unbound label is evaluated to the value “false”. In JAPE, RHS expressions involving unbound operators are not evaluated.
B.5 Classes [#]
The main external interfaces to JAPE are the classes gate.jape.Batch and gate.jape.Compiler. The CPSL Parser is implemented by ParseCpsl.jj, which is input to JavaCC (and JJDoc to produce grammar documentation) and finally Java itself. There are lots of other classes produced along the way by the compiler-compiler tools:
ASCII_CharStream.java JJTParseCpslState.java Node.java ParseCpsl.java
ParseCpslConstants.java ParseCpslTokenManager.java ParseCpslTreeConstants.java
ParseException.java SimpleNode.java TestJape.java Token.java TokenMgrError.java
These live in the parser subpackage, in the gate/jape/parser directory.
Each grammar results in an object of class Transducer, which has a set of Rule.
Constants are held in the interface JapeConstants. The test harness is in TestJape.
B.6 Implementation [#]
B.6.1 A Walk-Through [#]
The pattern application algorithm (which is either like Doug’s, or like Brill’s), makes a top-level call to something like
boolean matches(int position, Document doc,
MutableInteger newPosition) throws PostionOutOfRange |
which is a method on each Rule. This is in turn deferred to the rule’s LeftHandSide, and thence to the ConstraintGroup which each LeftHandSide contains. The ConstraintGroup iterates over its set of PatternElementConjunctions; when one succeeds, the matches call returns true; if none succeed, it returns false. The Rules also have
void transduce(Document doc) throws LhsNotMatched
|
methods, which may be called after a successful match, and result in the application of the RightHandSide of the Rule to the document.
PatternElements also implement the matches method. Whenever it succeeds, the annotations which were consumed during the match are available from that element, as are a composite span set, and a single span that covers the whole set. In general these will only be accessed via a bindingName, which is associated with ComplexPatternElements. The LeftHandSide maintains a mapping of bindingNames to ComplexPatternElements (which are accessed by array reference in Rule RightHandSides).
Although PatternElements give access to an annotation set, these are only built when they are asked for (caching ensures that they are only built once) to avoid storing annotations against every matched element. When asked for, the construction process is an iterative traversal of the elements contained within the element being asked for the annotations. This traversal always bottoms out into BasicPatternElements, which are the only ones that need to store annotations all the time.
In a RightHandSide application, then, a call to the LeftHandSide’s binding environment will yield a ComplexPatternElement representing the bound object, from which annotations and spans can be retrieved as needed.
B.6.2 Example RHS code
Let’s imagine we are writing an RHS for a rule which binds a set of annotations representing simple numbers to the label :numbers. We want to create a new annotation spanning all the ones matched, whose value is an Integer representing the sum of the individual numbers.
The RHS consists of a comma-separated list of blocks, which are either anonymous or labelled. (We also allow the CPSL-style shorthand notation as implemented in TextPro. This is more limiting than code, though, e.g. I don’t know how you could do the summing operation below in CPSL.) Anonymous blocks will be evaluated within the same scope, which encloses that of all named blocks, and all blocks are evaluated in order, so declarations can be made in anonymous blocks and then referenced in subsequent blocks. Labelled blocks will only be evaluated when they were bound during LHS matching. The symbol doc is always scoped to the Document which the Transducer this rule belongs to is processing. For example:
// match a sequence of integers, and store their sum Rule: NumberSum ( {Token.kind == "otherNum"} )+ :numberList --> :numberList{ // the running total int theSum = 0; // loop round all the annotations the LHS consumed for(int i = 0; i<numberListAnnots.length(); i++) { // get the number string for this annot String numberString = doc.spanStrings(numberListAnnots.nth(i)); // parse the number string and add to running total try { theSum += Integer.parseInt(numberString); } catch(NumberFormatException e) { // ignore badly-formatted numbers } } // for each number annot doc.addAnnotation( "number", numberListAnnots.getLeftmostStart(), numberListAnnots.getRightmostEnd(), "sum", new Integer(theSum) ); } // :numberList |
This stuff then gets converted into code (that is used to form the class we create for RHSs) looking like this:
package japeactionclasses;
import gate.*; import java.io.*; import gate.jape.*; import gate.util.*; import gate.creole.*; public class Test2NumberSumActionClass implements java.io.Serializable, RhsAction { public void doit(Document doc, LeftHandSide lhs) { AnnotationSet numberListAnnots = lhs.getBoundAnnots("numberList"); if(numberListAnnots.size() != 0) { int theSum = 0; for(int i = 0; i<numberListAnnots.length(); i++) { String numberString = doc.spanStrings(numberListAnnots.nth(i)); try { theSum += Integer.parseInt(numberString); } catch(NumberFormatException e) { } } doc.addAnnotation( "number", numberListAnnots.getLeftmostStart(), numberListAnnots.getRightmostEnd(), "sum", new Integer(theSum) ); } } } |
B.7 Compilation [#]
JAPE uses a compiler that translates CPSL grammars to Java objects that target the GATE API (and a regular expression library). It uses a compiler-compiler (JavaCC) to construct the parser for CPSL. Because CPSL is a transducer based on a regular language (in effect an FST) it deploys similar techniques to those used in the lexical analysers of parser generators (e.g. lex, flex, JavaCC tokenisation rules).
In other words, the JAPE compiler is a compiler generated with the help of a compiler-compiler which uses back-end code similar to that used in compiler-compilers. Confused? If not, welcome to the domain of the nerds, which is where you belong; I’m sure you’ll be happy here.
B.8 Using a Different Java Compiler [#]
GATE allows you to choose which Java compiler is used to compile the action classes generated from JAPE rules. The preferred compiler is specified by the Compiler_type option in gate.xml. At present the supported values are:
- Sun
- The Java compiler supplied with the JDK. Although the option is called Sun, it supports any JDK that supplies com.sun.tools.javac.Main in a standard location, including the IBM JDK (all platforms) and the Apple JDK for Mac OS X.
- Eclipse
- The Eclipse compiler, from the Java Development Tools of the Eclipse project2. Currently we use the compiler from Eclipse 3.2, which supports Java 5.0.
By default, the Eclipse compiler is used. It compiles faster than the Sun compiler, and loads dependencies via the GATE ClassLoader, which means that Java code on the right hand side of JAPE rules can refer to classes that were loaded from a plugin JAR file. The Sun compiler can only load classes from the system classpath, so it will not work if GATE is loaded from a subsidiary classloader, e.g. a Tomcat web application. You should generally use the Eclipse compiler unless you have a compelling reason not to.
Support for other compilers can be added, but this is not documented here - if you’re in a position to do this, you won’t mind reading the source code...
1By this we mean restrictions referring to the same type of annotations. If for branches 1-2 and 1-3 the restrictions for the type T1 are the same, the query for type T1 will be run only once. Each of the two branches can also have restrictions for other types of annotations.