Appendix F
IAA Measures for Classification Tasks [#]

IAA has been used mainly in the classification tasks, where two or more annotators are given a set of instances and are asked to classify those instances into some pre-defined categories. IAA measures the agreements among the annotators on the class labels assigned to the instances by the annotators. Text classification tasks include document classification, sentence classification(e.g. opinionated sentence recognition), and token classification (e.g. POS tagging).

The three commonly used IAA measures are observed agreement, specific agreement, and Kappa (κ) [Hripcsak & Heitjan 02]. Those measures can be calculated from a contingency table, which lists the numbers of instances of agreement and disagreement between two annotators on each category. To explain the IAA measures, a general contingency table for two categories cat1 and cat2 is showed in Table F.1.

Observed agreement is the portion of the instances on which the annotators agree. For the two annotators and two categories as shown in Table F.1, it is defined as

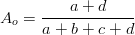
(F.1)

The extension of the above formula to more than two categories is in straight way. The extension to more than two annotators is usually taken as the mean of the pair-wise agreements [Fleiss 75], which is the average agreement across all possible pairs of annotators. An alternative compares each annotator to the majority opinion of the others [Fleiss 75].

However, the observed agreement has two shortcomings. One is that certain amount of agreement is expected by chance. The Kappa measure is a chance-corrected agreement. Another is that it sums up the agreement on all the categories but the agreements on each category may differ. Hence the category specific agreement is needed.

Specific agreement quantifies the degree of agreement for each of the categories separately. For example, the specific agreement for the two categories list in Table F.1 is the following, respectively,

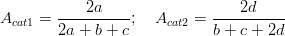
(F.2)

Kappa is defined as the observed agreements A_o subtracted by the agreement expected by chance A_e and is normalized as a number between -1 and 1.

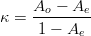
(F.3)

κ = 1 means perfect agreements, κ = 0 means the agreement is equal to chance, κ = -1 means ”perfect” disagreement.

There are two different ways of computing the chance agreement A_e (for a detailed explanations about it see [Eugenio & Glass 04]). The Cohen’s Kappa is based on the individual distribution of each annotator, while the Siegel & Castellan’s Kappa is based on the assumption that all the annotators have the same distribution. The former is more informative than the latter and has been used widely.

The Kappa suffers from the prevalence problem which arises because imbalanced distribution of categories in the data increases A_e. The prevalence problem can be alleviated by reporting the positive and negative specified agreement on each category besides the Kappa [Hripcsak & Heitjan 02, Eugenio & Glass 04]. In addition, the so-called bias problem affects the Cohen’s Kappa, but not S&C’s. The bias problem arises as one annotator prefers to one particular category more than another annotator. [Eugenio & Glass 04] advised to compute the S&C’s Kappa and the specific agreements along with the Cohen’s Kappa in order to handle the problems.

Despite the problem mentioned above, the Cohen’s Kappa remains a popular IAA measure. Kappa can be used for more than two annotators based on pair-wise figures, e.g. the mean of all the pair-wise Kappa as an overall Kappa measure. The Cohen’s Kappa can also be extended to the case of more than two annotators by using the following single formula [Davies & Fleiss 82]

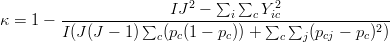
(F.4)

Where I and J are the number of instances and annotators, respectively; Y _ic is the number of annotators who assigns the category c to the instance I; p_cj is the probability of the annotator j assigning category c; p_c is the probability of assigning category by all annotators (i.e. averaging p_cj over all annotators).

S&C’s Kappa is applicable for any number of annotators. S&C’s Kappa for two annotators is also known as Scott’s Pi (see [Lombard et al. 02]). The Krippendorff’s alpha, another variant of Kappa, differs only slightly from the S&C’s Kappa on nominal category problem (see [Carletta 96, Eugenio & Glass 04]).

However, note that the Kappa (and the observed agreement) is not applicable to some tasks. Named entity annotation is one of such tasks [Hripcsak & Rothschild 05]. In named entity annotation task, annotators are given some text and are asked to annotate some named entities (and possible their categories) in the text. Different annotators may annotate different instances of named entity. So, if one annotator annotates one named entity in the text but another annotator does not annotate it, then that named entity is a non-entity for the latter. However, generally the non-entity in text is not a well-defined term, e.g. we don’t know how many words should be contained in non-entity. On the other hand, if we want to compute Kappa for named entity annotation, we need the non-entities. That’s why people doesn’t compute Kappa for named entity task.